
Un graphe est un ensemble de points appelés nœuds et des relations entre ces nœuds appelées arêtes. Cette définition simple ouvre de nombreuses variantes. Les arêtes peuvent être orientées (c’est-à-dire admettre une direction) ou non, deux nœuds peuvent être reliés au maximum par une seule arête ou plusieurs. De plus les nœuds ou les arêtes peuvent être enrichis par des données supplémentaires ; la plupart du temps, des informations liés à l’entité que représente un nœud ou, pour une arête, un nombre qui représente l’intensité du lien entre les nœuds reliés par cette arête.
Les graphes apparaissent dans de nombreuses situations.
En chimie, comme illustré par le diagramme ci-dessus, une molécule forme un graphe dont les nœuds sont les atomes et les arêtes sont les liaisons. Ces liaisons peuvent être de deux types : les liaisons doubles représentées par deux traits parallèles et les liaisons simples représentées par un seul trait [1].
Une triangulation d’une surface (et plus généralement d’une variété mathématique) produit un graphe. Des phénomènes physiques peuvent dès lors se décrire sous la forme de graphe. Par exemple, dans le cas de la météo mondiale, la terre forme une sphère que l’on peut trianguler et obtenir ainsi un graphe. On peut associer à chaque nœud de ce graphe un vecteur qui représente les conditions météorologiques locales [2].

L’univers des relations sociales offre une grande variété de graphes. Ainsi, l’image suivante, mise en forme par John Decker d’après des données rassemblées par John Padgett [3] , représente les grandes familles florentines du 15ème siècle et leur relations maritales. Plus une famille est fortunée et plus le disque associé est grand [4].
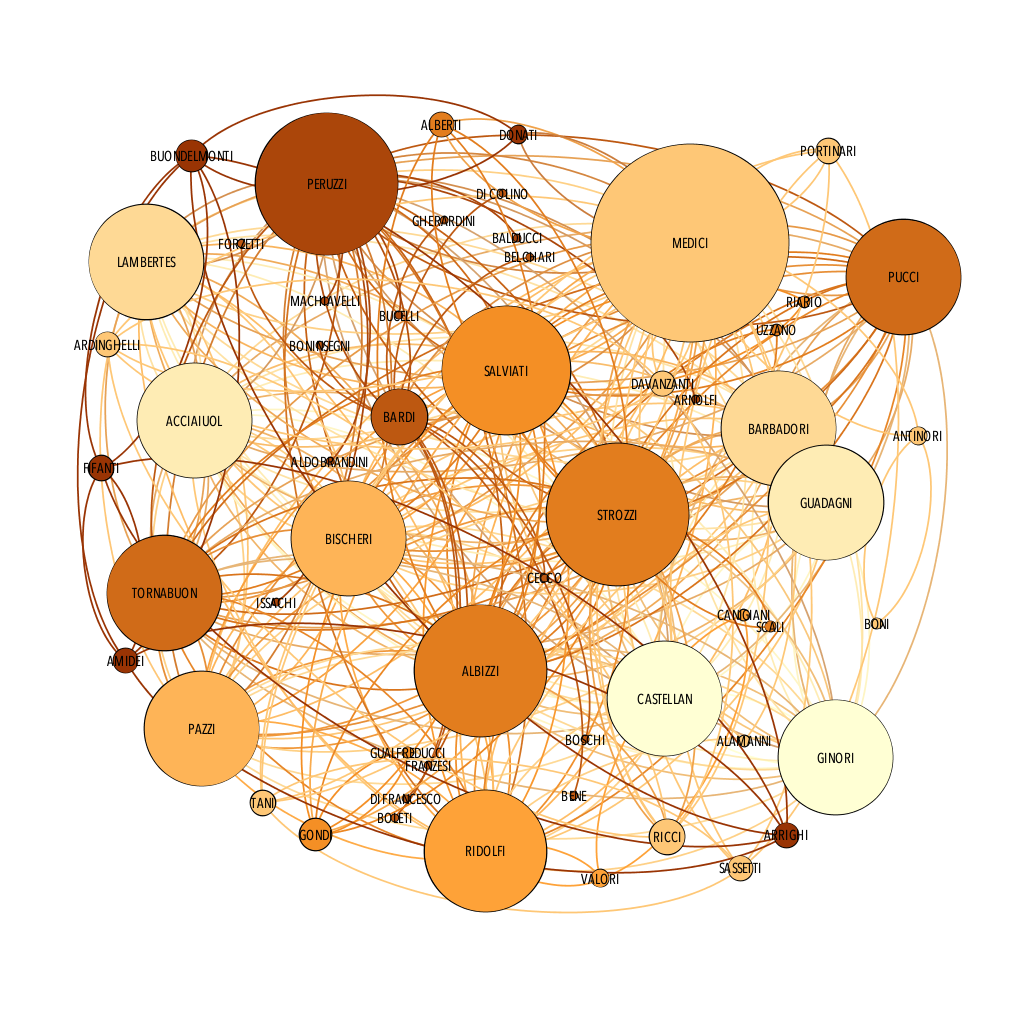
Un réseau social (Facebook, LinkedIn, …) forme un graphe : les nœuds sont les utilisateurs et une arête les relient dès qu’ils sont liés sur le réseau social. Ce lien peut être enrichi de nombres décrivant la force de l’interaction (par exemple, le nombre de messages échangés).
Concentrons-nous sur le monde des paiements et des transactions qui est le cœur de métier d’Heptalytics. A partir d’un seul réseau d’échange, on peut construire plusieurs graphes. D’une part, un graphe de transactions, dont les nœuds sont les transactions et les agents économiques et dont les arêtes relient ces transactions à leurs émetteurs et récepteurs. D’autre part, un graphe d’agents économiques dont les nœuds sont ces mêmes agents et les arêtes décrivent les flux économiques entre eux.
Ces structures en graphes amènent des questions de classification ou de régression.
Par exemple, on peut chercher à qualifier les nœuds d’un graphe. Dans le cas d’un réseau d’échange d’argent, un nœud peut représenter une transaction ou un agent économique. Une transaction peut être frauduleuse ou non, tout comme un agent économique peut être un fraudeur ou non. Dans le cas de la météo globale, on peut également chercher à prédire le temps qu’il fera dans 24 heures en chaque point du graphe de triangulation.
On peut chercher à qualifier le un graphe tout entier. Par exemple, pour une protéine, on peut essayer de quantifier son affinité avec une molécule dans le cadre de la recherche de médicaments.
On peut enfin chercher à qualifier les arêtes d’un graphe. Par exemple, dans un réseau social, à quel point une relation précise entre deux personnes est-elle une relation significative ?
Pour traiter ces problèmes, notamment dans la détection de fraude chez Heptalytics, il nous faut des algorithmes de Machine Learning adaptés aux graphes. C’est là qu’entrent en jeu les réseaux de neurones en graphe ou GNN (graph neural networks).
[1] Généré par Wolfram Mathematica.
[2] Wikipédia https://fr.wikipedia.org/wiki/G%C3%A9ode_(g%C3%A9om%C3%A9trie)
[3] http://www.casos.cs.cmu.edu/computational_tools/datasets/external/padgett/index2.html
[4] https://studentwork.prattsi.org/infovis/labs/visualizing-florentine-family-networks/


