
En Machine Learning, les réseaux de neurones sont construits à partir de briques fonctionnelles tels que les couches denses, les mécanismes d’attention, les couches de convolution etc.
Dans cet article nous décrivons les briques qui forment les réseaux de neurones en graphes appelés GNN (pour Graph Neural Networks).
Couche de transmission de messages (message passing layer)[1][2]
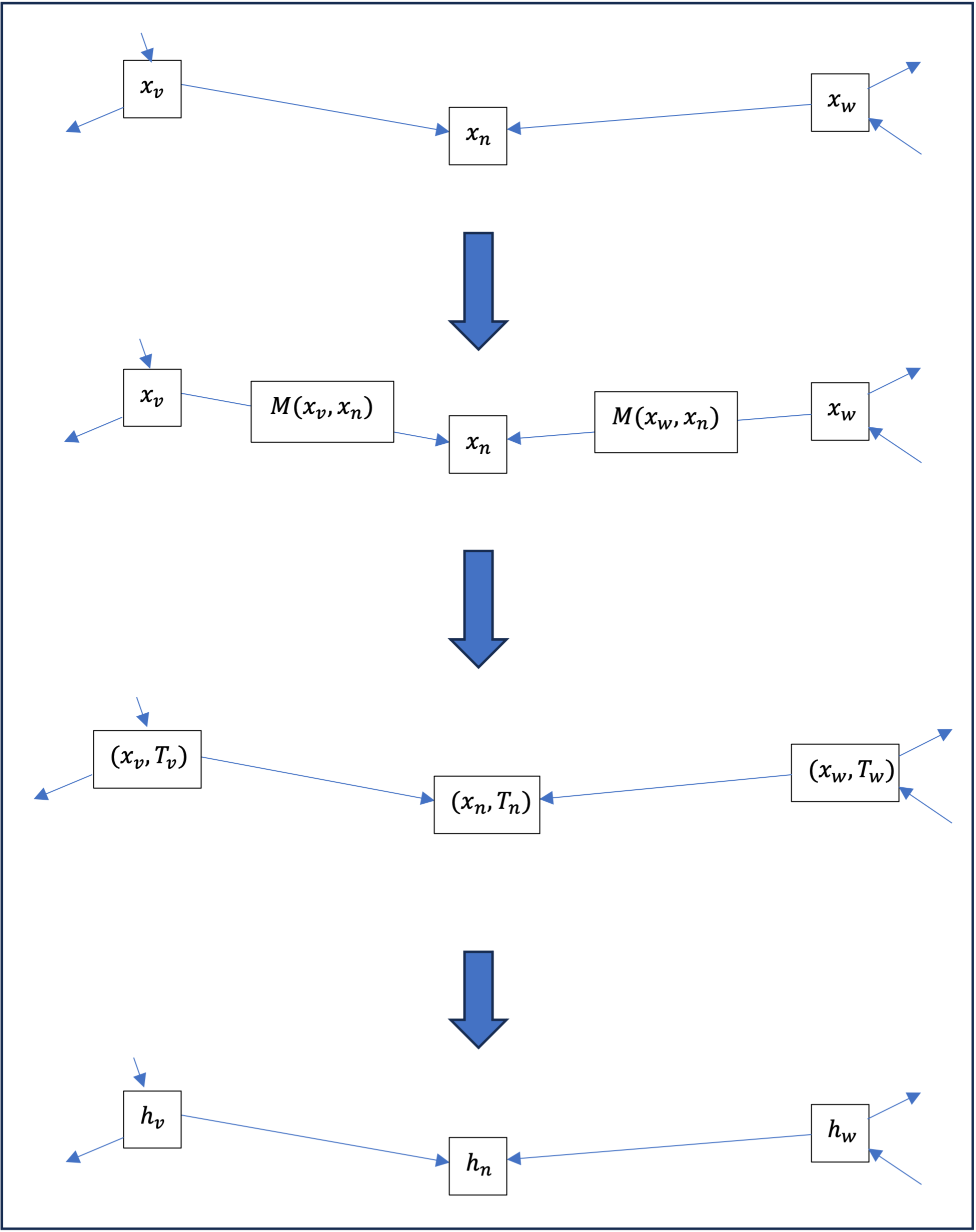
Considérons un graphe \ ( G \ ) et pour chaque nœud \ ( n \ ) , un vecteur ( x_n \ in \mathbb{R}^{m} ) . Au sens large, une couche de transmission de messages est une fonction qui pour chaque nœud \ ( n \ ) va construire un nouveau vecteur ( h_n \in \mathbb{R}^{m'} ) à partir d’une part du vecteur (x_n\ ) et d’autre part des vecteurs \ ( x_v\ ) pour tout nœud \ ( v\ ) voisin de \ ( n\ ) , de la façon suivante :
- Pour chaque nœud \ ( v\ ) voisin de \ ( n \ ) , on calcule le message de \ ( v\ ) vers \ ( n \ ) comme une fonction \ (M \ ) de ( x_n\ ) et ( x_v\ ) :
\mathrm{Message}_{\{v \to n\}}= M(x_v, x_n). - Tous ces messages sont agrégés en une transmission ( T_n\ ) reçue par le nœud \ ( n \ ) , chaque message individuel étant traité sur un même pied d’égalité ; autrement dit l’agrégation est invariante par permutation des messages[3] ; cela se fait habituellement en sommant les messages
T_n = \sum_v M(x_v, x_n),
ou en les moyennant
T_n = \frac{1}{N} \sum_v M(x_v, x_n),
Sachant que les deux sommes sont prises sur l’ensembles des voisins [/latex] \ ( v\ ) [/latex] de \ ( n \ ) et que \ ( N\ ) est la taille de cet ensemble, c’est-à-dire le nombre de voisins de \ ( n \ ) . - Enfin \ ( h_n\ ) est calculé comme fonction \ ( P\ ) du vecteur \ ( x_n\ ) et de la transmission \ ( T_n\ ) :
h_n = P\!\left(x_n, T_n\right)\!.
Cas d’application : la convolution
L’exemple typique d’une couche de transmission de messages est la couche dite de convolution[4] où la fonction \ ( M\ ) renvoie juste le vecteur source du message et l’agrégation est la somme et la fonction \ ( P\ ) est une fonction affine suivie d’une fonction d’activation M\!\left(x,y\right) = x; \\ P\!(x,T) = \sigma\!\left(\!\left(x,T\right)\!A + b\right)\!.
On peut également considérer des variations de ce principe de transmission de message, notamment dans le cas où les arêtes sont enrichies par des valeurs qui peuvent entrer en jeu dans le calcul. Citons également la couche d’attention[5] (ou Transformer) où le message est calculé en deux fois, la première servant à calculer un coefficient dit coefficient d’attention pour chaque nœud \ ( v\ ) voisin de \ ( n\ ) qui est normalisé par rapport à l’ensemble de ces voisins \alpha\!\left(x_v, x_n\right) = \frac{e^{A\left(x_v, x_n\right)}}{\sum_w e^{A\left(x_w, x_n\right)}}, où \ ( A\ ) est une fonction bilinéaire et où la somme est prise sur l’ensemble des nœuds \ ( w\ ) voisins de \ ( n\ ). On calcule ensuite le message d’un nœud voisin \ ( v\ ) vers le nœud \ ( n\ ) M\!\left(x,y\right) = \alpha\!\left(x_v, x_n\right)V\!\left(x_v\right) comme le produit du coefficient d’attention et d’une fonction \ ( V\ ) affine.
Ainsi, un exemple de méthode de classification de nœuds d’un graphe \ ( G\ ) est d’appliquer successivement :
- plusieurs couches de transmission de messages ;
- puis, une ou plusieurs couches denses sur chaque vecteur associé à un nœud.
Mutualisation (pooling)[6]
La couche de transmission de message (ou ses variations) nous suffit à construire des classifieurs de nœuds d’un graphe. Cependant, elle ne permet de construire des classifieurs de graphes entiers. Pour cela on peut utiliser une couche, ou comme on va le voir, plusieurs couches de mutualisation.
La mutualisation est une opération qui, à partir d’un graphe \ ( G\ ) dont pour chaque nœud \ ( n\ ) est enrichi d’un vecteur \ ( x_n \in \mathbb{R}^{m}\ ), produit un nouveau vecteur \ ( y_G \in \mathbb{R}^{m'}\ ) associé au graphe en entier. Les méthodes de mutualisation les plus utilisées sont la somme y_G=\sum_n x_n, la moyenne y_G=\frac{1}{N}\sum_n x_n, ou le maximum y_G=\max_n x_n.
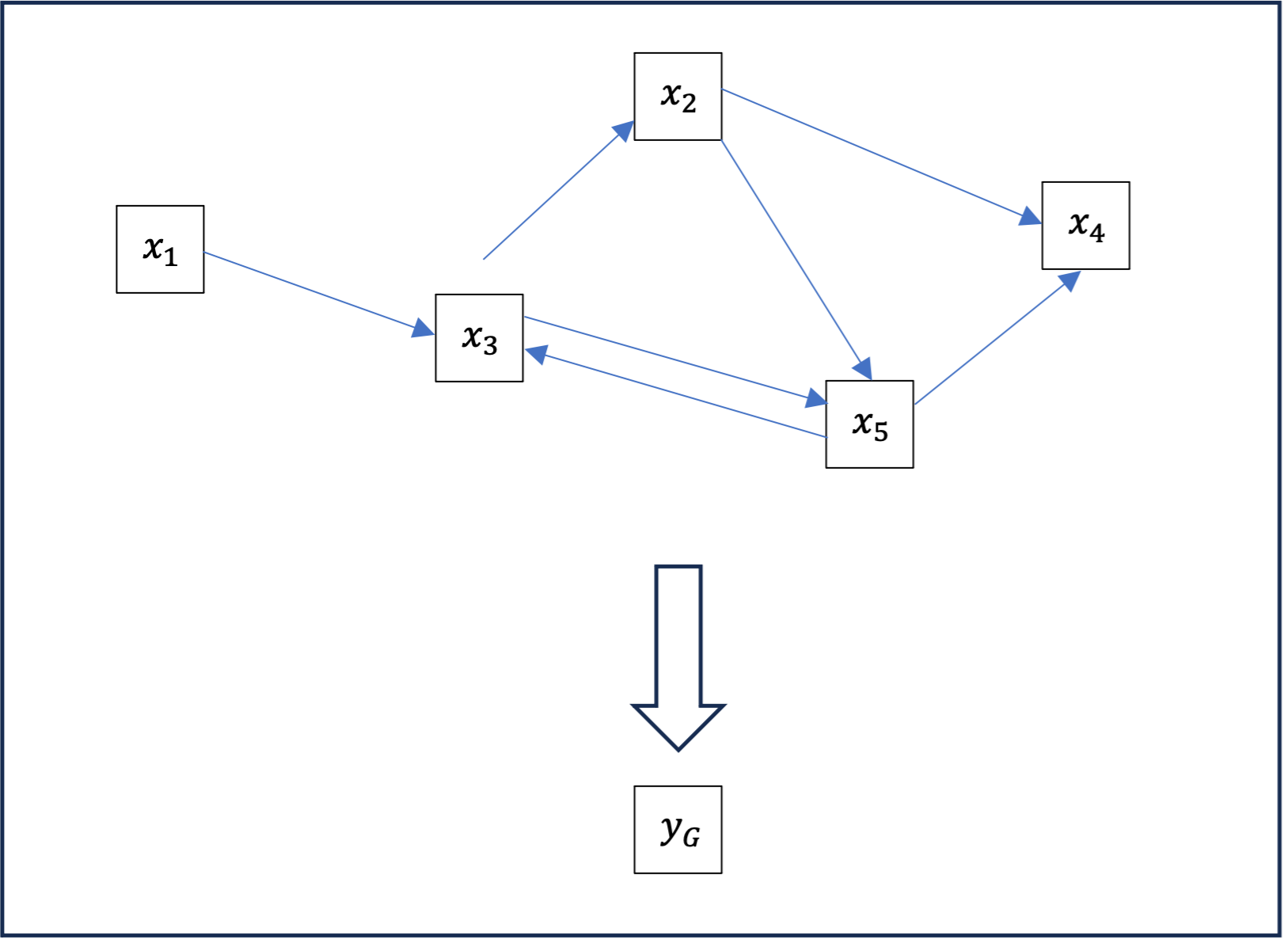
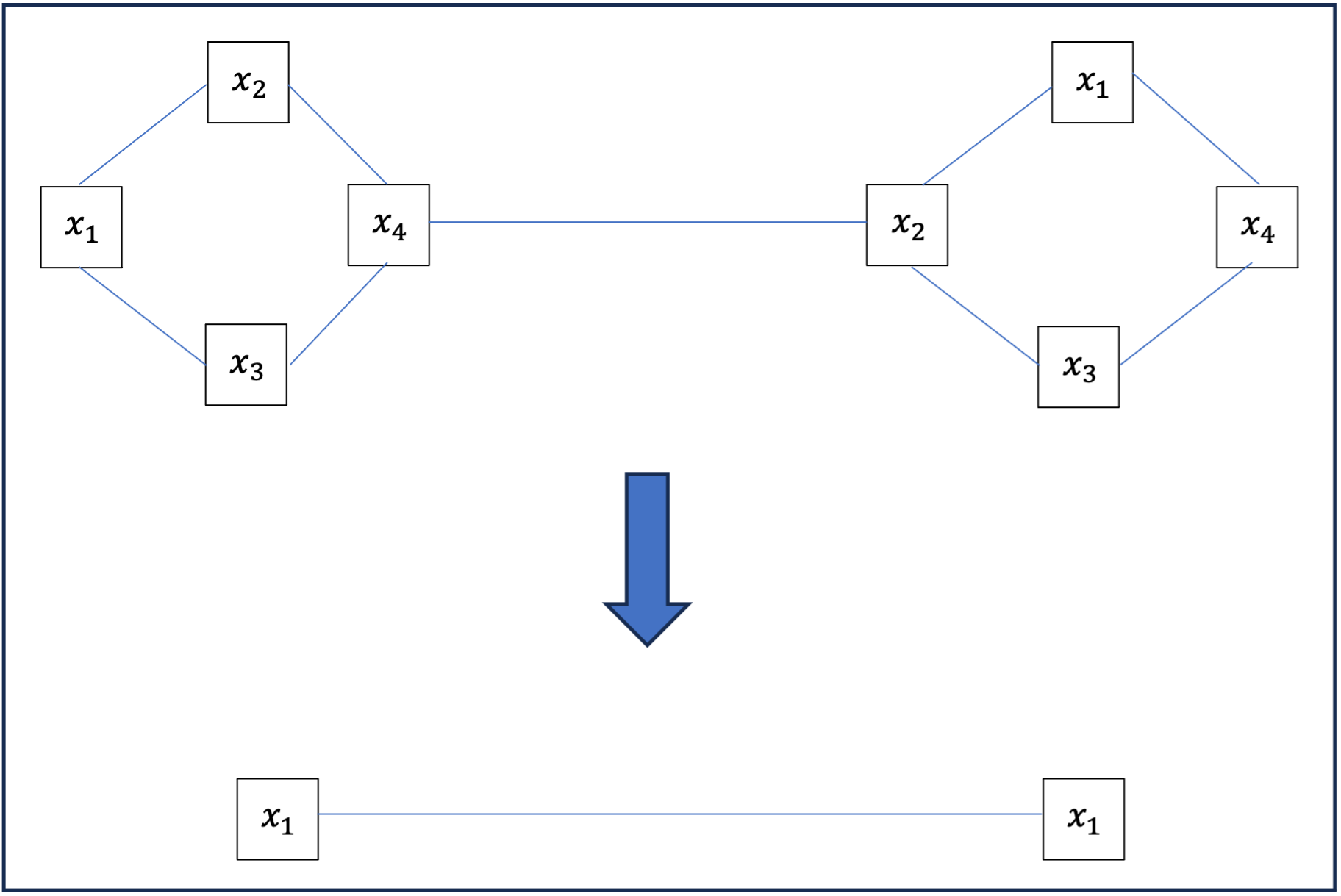
Cette opération de mutualisation peut paraître abrupte ; pour un graphe important, on passe de la donnée de nombreux vecteurs et de relations complexes entre eux à un seul vecteur de même dimension. Dans de nombreux cas, on ne va pas mettre en œuvre cette opération sur le graphe complet mais sur des clusters du graphe ; on obtient alors nouveau graphe dont les nœuds sont les clusters du précédent à la manière de l’exemple suivant où y_{1,2,3,4} = \sum_{1}^4 x_i, \\ y_{5,6,7,8} = \sum_{5}^8 x_i.
Optimisation de la classification de graphes
Ainsi, un exemple de méthode de classification de graphes est d’appliquer successivement sur un graphe \ ( G\ ) :
- plusieurs couches de transmission de messages ;
- une mutualisation par clusters ;
- à nouveau plusieurs couches de transmission de messages sur le graphe des clusters ;
- une mutualisation globale ;
- enfin, une ou plusieurs couches denses sur le vecteur mutualisé.
Cette méthode de calcul et application des réseaux de neurones en graphes est utilisée chez Heptalytics. pour lutter contre la fraude, et établir le scoring fraude & LCBFT.
[1] Justin Gilmer, Samuel S. Schoenholz, Patrick F. Riley, Oriol Vinyals, and George E. Dahl. 2017. Neural message passing for Quantum chemistry. In Proceedings of the 34th International Conference on Machine Learning – Volume 70 (ICML’17). JMLR.org, 1263–1272
[2] L. Wu, P. Cui, J. Pei, and L. Zhao. Graph Neural Networks: Foundations, Frontiers, and Applications. Springer, Singapore, 2022, section 4.2.
[3] Euan Ong, Petar Veličković Proceedings of the First Learning on Graphs Conference, PMLR 198:43:1-43:22, 2022.
[4] Kipf TN, Welling M. Semi-supervised classification with graph convolutional networks. In: 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, April 24-26, 2017, Conference Track Proceedings, OpenReview.net
[5] Voir Veličković, P., Casanova, A., Liò, P., Cucurull, G., Romero, A., & Bengio, Y. (2018). Graph attention networks. OpenReview.net. https://doi.org/10.17863/CAM.48429
[6] L. Wu, P. Cui, J. Pei, and L. Zhao. Graph Neural Networks: Foundations, Frontiers, and Applications. Springer, Singapore, 2022, section 9.3.


